Graphical Abstract

• Tweet

Yamamoto, H., and S. Yoden, 2013: Theoretical estimation of the superrotation strength in an idealized quasi-axisymmetric model of planetary atmospheres. J. Meteor. Soc. Japan, 91, 119-141.
https://doi.org/10.2151/jmsj.2013-203

• Graphical Abstract with highlights
• Original PDF

Highlights:

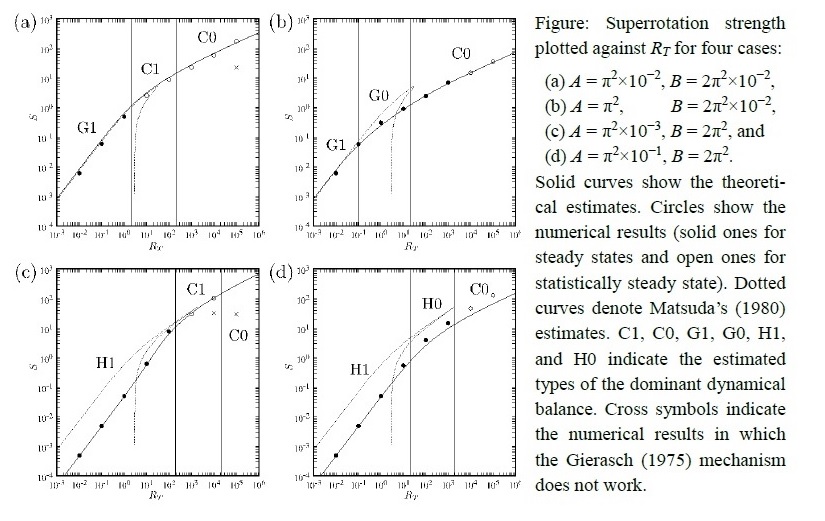
• This paper presents a theoretical estimation of the strength of equatorial superrotation in planetary atmospheres by exploring quasi-axisymmetric primitive equations with the effects of non-axisymmetric eddies parameterized by strong horizontal eddy diffusion. In this system, the superrotation is maintained by the Gierasch (1975) mechanism.
• A quintic equation for the superrotation strength is developed from the primitive equations; estimates are given by its unique positive solution. The solution depends only on three non-dimensional parameters: the external thermal Rossby number (R_T), the ratio of the radiative relaxation time to the timescale for the vertical diffusion (A=π² τ Ω E_V), and the square of the ratio of the planetary rotation period to the geometric mean of the timescales for the horizontal and vertical diffusion (B=20 π² E_HE_V).
• The parameter dependence of the dominant dynamical balance is also investigated. The balance is a cyclostrophic (C·), geostrophic (G·), or horizontal diffusion balance (H·), and in each balance, the equator-to-pole temperature difference is either nearly equal to that in radiative-convective equilibrium state (·1) or significantly reduced by thermal advection (·0).
• Numerical solutions of the primitive equations are obtained for a wide parameter range and the obtained superrotation strength (solid and open circles in the figure) agrees well with the theoretical estimation (solid curves), showing the validity of the present theory.