Graphical Abstract

• Tweet

Noda, A., 2014: Generalized transformed Eulerian mean (GTEM) description for Boussinesq fluids. J. Meteor. Soc. Japan, 92, 411-431.
https://doi.org/10.2151/jmsj.2014-501

• Graphical Abstract with highlights
• Original PDF

Highlights:

• A generalized transformed Eulerian mean (GTEM) set of equations is derived based on a nonneutral (unstable/dissipative) wave under dissipation and/or diabatic heating conditions in a Boussinesq stratified fluid.
• The key quantity that characterizes the GTEM is the eddy diffusion tensor. The conventional transformed Eulerian means (TEMs) are shown to be based on simplified forms of the antisymmetric components of the eddy diffusion tensor in the framework of the GTEM. The full components are derived based on the waveform. However, the explicit form of the wave frequency and wavenumber of eddies is not referred to so as to apply the GTEM to actual atmospheric and oceanic data analyses.
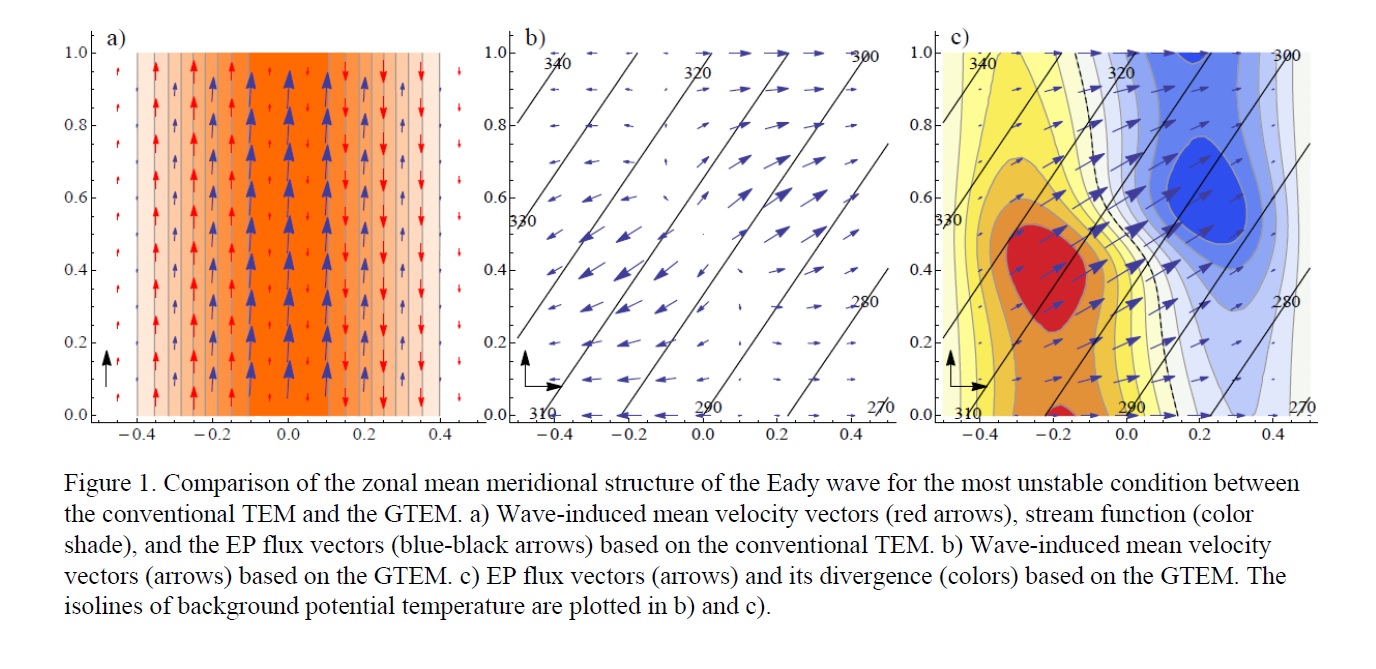
• The wave-induced transport velocity, which is defined as the divergence of the eddy diffusion tensor, is nondivergent by definition for that originated from the antisymmetric components, but divergent in general for that originated from the symmetric components. The focal mechanism that induces the difference and the Lagrangian mean motion, i.e., the Stokes drift defined in the generalized Lagrangian mean (GLM), is illustrated by figures.
• The Eliassen-Palm flux is originally defined in terms of the covariance of velocity and pressure perturbations and has a clear physical meaning of the wave momentum transport via group velocity for the waves that satisfy appropriate conditions in the GTEM formulation. However, it can be calculated as the residual of the Reynolds stress minus other terms relevant to the eddy diffusion tensor.
• An application to the Eady unstable wave is made to illustrate the differences between TEM, GLM, and GTEM, and the importance of the symmetric part of the eddy diffusion tensor (Fig. 1).