Graphical Abstract

• Tweet

Duc, L., K. Saito, and D. Hotta, 2020: An explanation for the diagonally predominant property of the positive symmetric ensemble transform matrix. J. Meteor. Soc. Japan, 98, 455-462.
https://doi.org/10.2151/jmsj.2020-022
Graphical Abstract

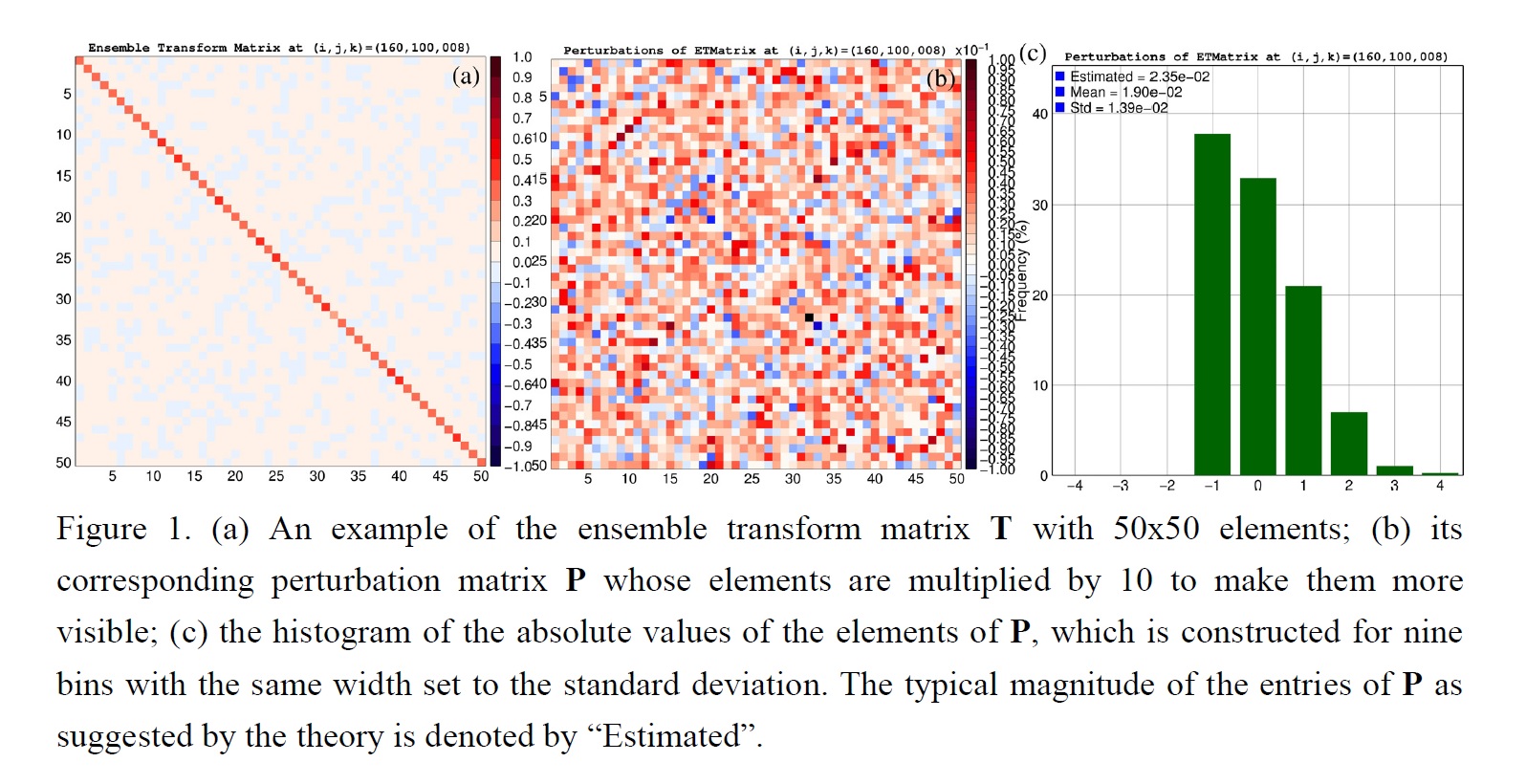
Plain Language Summary: The ensemble transform matrix T in the Ensemble Transform Kalman Filter is observed to have the diagonally predominant property, i.e. the diagonal terms are at least an order of magnitude larger than the off-diagonal terms, but why it possesses such a property has not been well understood. This property has shown to have a close connection to the fact that T is the closest matrix to a scalar multiple of the identity I. This fact reveals that T can be decomposed into a sum of a diagonal matrix D and a full matrix P whose Frobenius norms are proportional, respectively, to the mean and the standard deviation of the spectrum of T. In general cases, these norms are not much different but the fact that the number of non-zero elements of P is the square of ensemble size while that of D is the ensemble size causes the large difference in the orders of elements of P and D.

Highlights:

• T is proved to be the closest matrix to the identity I in the sense of the Frobenius norm among all valid ensemble transform matrices. This property has been stated but never proved in the data assimilation literature.
• T is also proved to be the closest matrix to a scalar multiple of I. The scalar multiple of I closest to T in this case is aI where a is the average of the eigenvalues of T.
• The diagonally predominant property is only an empirical fact and not an inherently mathematical property of T. Violations of this property are rarely observed in practice since their occurrences require an unrealistic situation where background errors are larger than observation errors by at least two orders of magnitude.