Graphical Abstract

• Tweet

Steppeler, J., J. Li, F. Fang, and J. Zhu, 2021: The o2o3 Local Galerkin method using a differentiable flux representation. J. Meteor. Soc. Japan, 100, 9-27.
https://doi.org/10.2151/jmsj.2021-077
Graphical Abstract Published

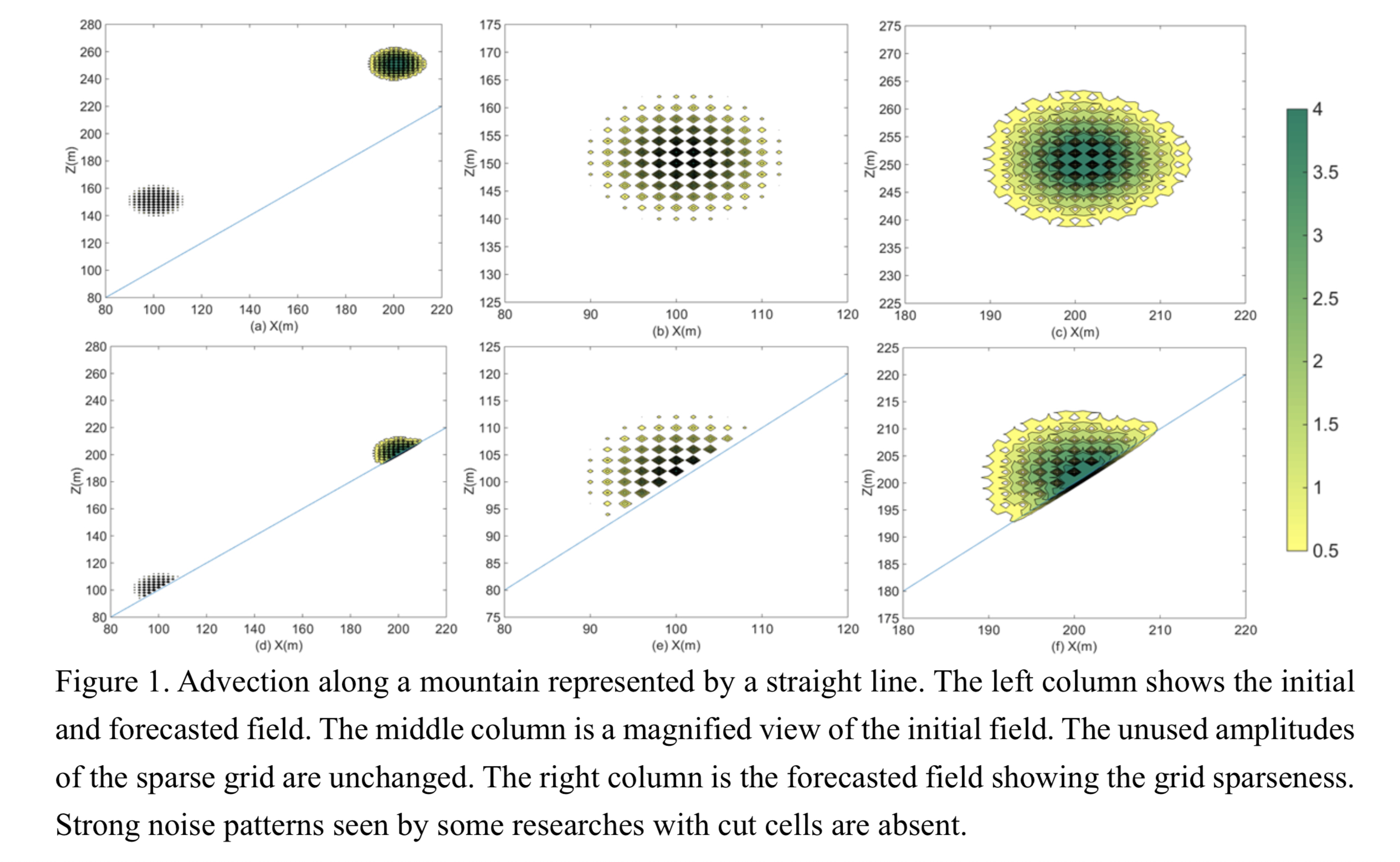
Plain Language Summary: Local Galerkin methods, in particular the spectral elements (SE) solve the difficulty in classic Galekin methods for applying to multiprocessor system and have been found to be scalable up to millions of processors. The present study investigates improvements of SE under the name o2o3 which substitutes the irregular Gauss-Lobatto grid in SE by a regular collocation grid to compute Galerkin integrals with the potential to improve the computational efficiency and simplify the physical parameterization.
 

• Original PDF

Highlights:

• The accuracy of o2o3 is comparable to that of third-order SE (SE3) as a result of the constructed superconvergence.
• Compared with SE3, o2o3 utilizes a regular grid enabling to use a larger time step with the potential to generate sparse grids and improve the computational efficiency even when parameterizing physical processes.
• o2o3 is suitable to formulate lower boundary conditions for irregular surfaces, thus allowing to formulate the high-order cut-cell approximation.