Graphical Abstract

• Tweet

Ishioka, K., N. Yamamoto, and M. Fujita, 2022: A formulation of a three-dimensional spectral model for the primitive equations. J. Meteor. Soc. Japan, 100, 445-469.
https://doi.org/10.2151/jmsj.2022-022.
Graphical Abstract Published

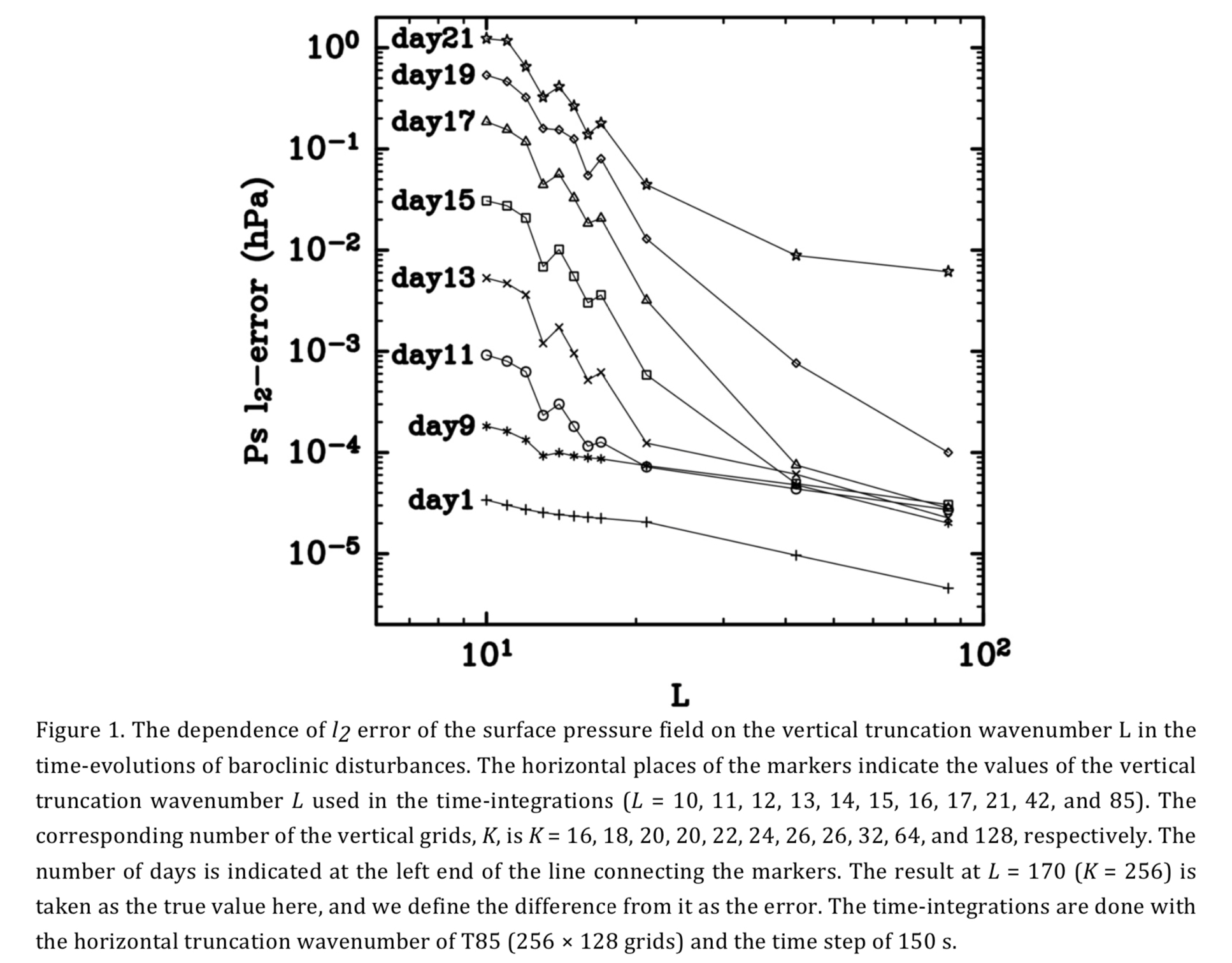
Plain Language Summary: A formulation of a three-dimensional spectral model based on the primitive equations is proposed. In this formulation, the Legendre polynomial expansion is used for the vertical discretization. By performing several calculations with different vertical degrees of freedom, a characteristic property of the spectral method is observed in which the error of the numerical solution decreases rapidly when the number of vertical degrees of freedom is increased.  

Highlights:

• Semi-implicit time integration can be efficiently done under this formulation.
• This implementation of the primitive equations can give accurate numerical solutions with a relatively small degrees of freedom in the vertical discretization.
• An alternative to the sponge layer can be devised to suppress the reflected waves under this formulation.