Graphical Abstract

• Tweet

Duc, L., Y. Sawada, 2024: Geometry of rainfall ensemble means: from arithmetic averages to Gaussian-Hellinger barycenters in unbalanced optimal transport. J. Meteor. Soc. Japan, 102.
https://doi.org/10.2151/jmsj.2024-003
Early Online Release   Graphical Abstract New GA

Plain Language Summary: It is well-known in rainfall ensemble forecasts that ensemble means suffer substantially from the diffusion effect resulting from the averaging operator. Therefore, ensemble means are rarely used in practice. This study has used the limitation of ensemble means as evidence to support the viewpoint that the geometry of rainfall distributions is not the familiar Euclidean space but a different space. The rigorously mathematical theory underlying this space has already developed in the theory of unbalanced optimal transport. This geometry is associated with the Gaussian-Hellinger distance. This distance is the optimal cost to push a source distribution to a destination distribution with penalties on the mass discrepancy between mass transportation and original mass distributions. In the new geometry, ensemble means are identified with Gaussian-Hellinger barycenters, and the diffusion effect, as in the case of arithmetic means, is avoided. The new ensemble means being placed side-by-side with deterministic forecasts provide useful information for forecasters in decision-making.

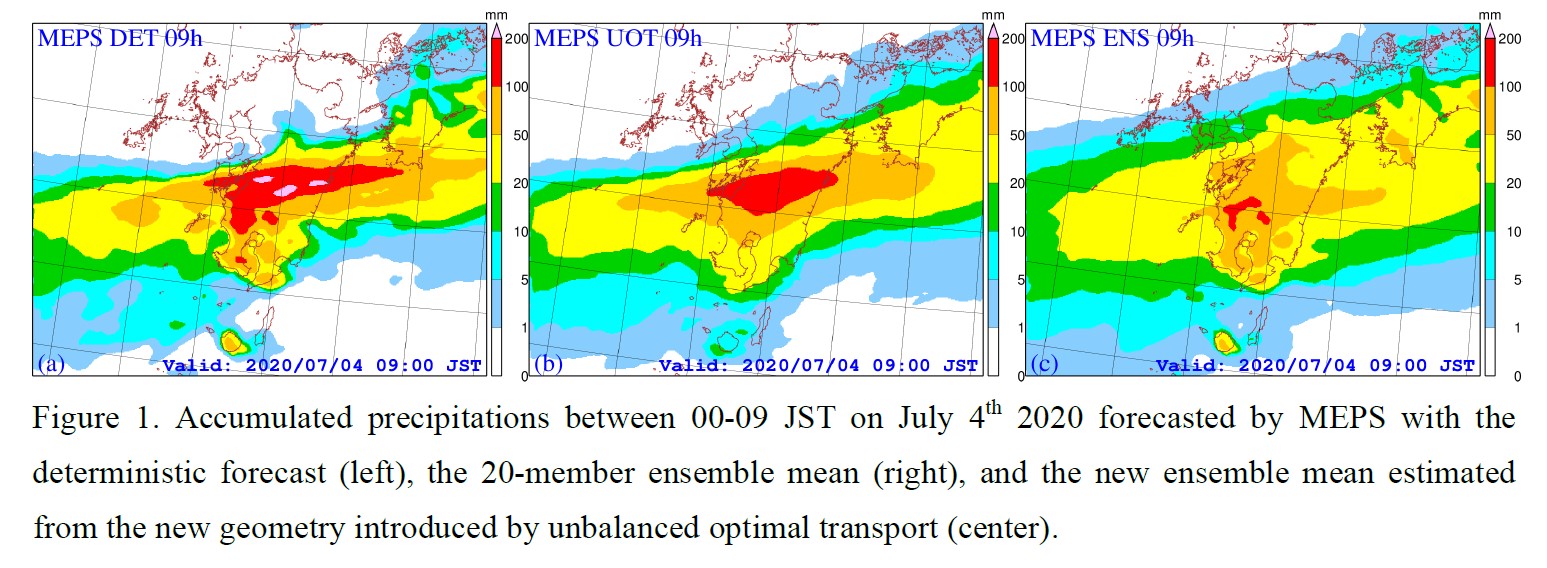
Highlights:

• Ensemble forecast results are usually announced using ensemble means. However, for the rainfall variable, ensemble means are rarely used in practice due to the diffusion effect resulting from the averaging operator, which smooths rainfall significantly.
• A method to calculate more meaningful ensemble means of rainfall is proposed based on the theory of unbalanced optimal transport. The new ensemble means are interpreted as barycenters of rainfall distributions with respect to a new geometric distance called the Gaussian-Hellinger distance.
• The new ensemble means avoid the diffusion effect as observed in the case of arithmetic means, and open a way to reintroduce ensemble means of rainfall back to numerical weather prediction.