JMSJ Highlights

Editor's Highlight : Rojahn et al. (2023)

Rojahn A., N. Schenk, P.-J. van Leeuwen and P. Roland, 2023: Particle filtering and gaussian mixtures - On a Localized Mixture Coefficients Particle Filter (LMCPF) for global NWP. J. Meteor. Soc. Japan, 101.
https://doi.org/10.2151/jmsj.2023-015.
Early Online Release Graphical Abstract

Editor in charge: Dr. Takuya Kawabata

A particle filter (PF) in the global NWP at DWD is proposed and evaluated its skills in comparison with the operational system.
To alleviate the degeneration, which is the largest issue in PFs with high-dimensional systems, several approaches are effectively incorporated such as localization, Gaussian mixture approximation in the prior distribution, adaptive resampling, and so on (See Section 2.3).
Since comprehensive formulations in this system are described, the readers can totally understand its theoretical aspects.

Abstract
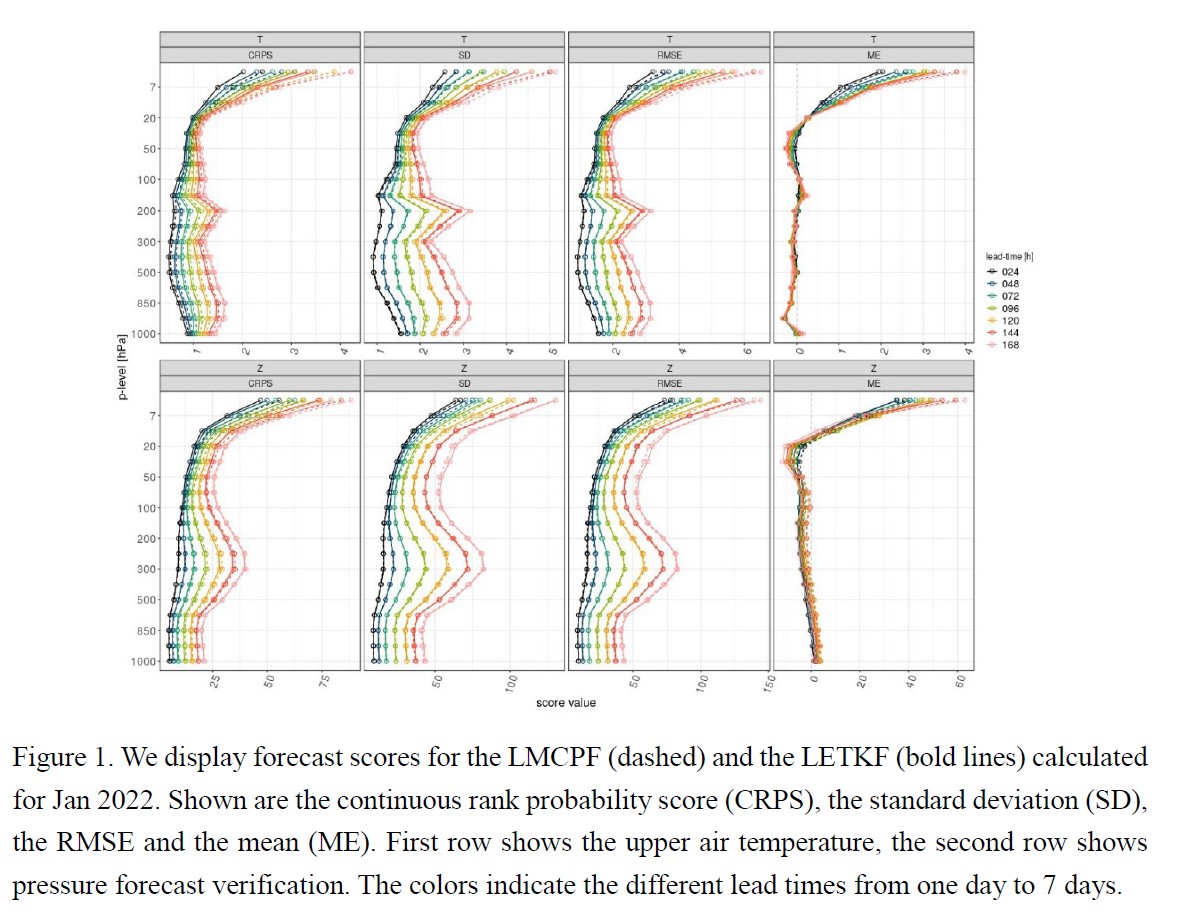
In a global numerical weather prediction (NWP) modeling framework we study the implementation of Gaussian uncertainty of individual particles into the assimilation step of a localized adaptive particle filter (LAPF). We obtain a local representation of the prior distribution as a mixture of basis functions. In the assimilation step, the filter calculates the individual weight coefficients and new particle locations. It can be viewed as a combination of the LAPF and a localized version of a Gaussian mixture filter, i.e., a Localized Mixture Coefficients Particle Filter (LMCPF).
Here, we investigate the feasibility of the LMCPF within a global operational framework and evaluate the relationship between prior and posterior distributions and observations. Our simulations are carried out in a standard pre-operational experimental set-up with the full global observing system, 52 km global resolution and 106 model variables. Statistics of particle movement in the assimilation step are calculated. The mixture approach is able to deal with the discrepancy between prior distributions and observation location in a real-world framework and to pull the particles towards the observations in a much better way than the pure LAPF. This shows that using Gaussian uncertainty can be an important tool to improve the analysis and forecast quality in a particle filter framework.